Nederlandstalige Journal Club

<<Terug naar de hoofdpagina

Hier vind je een alfabetische verklarende woordenlijst van termen die je in klinische studies of andere wetenschappelijk publicaties kan tegenkomen. Onderaan kan je een reactie achterlaten, als je b.v.b. een vraag hebt over een bepaalde term die je bent tegengekomen in onze artikels of bij eigen opzoekwerk.

• 2×2 factorial design: studie waarbij 2 interventies zowel elk apart als in combinatie worden bestudeerd tegenover geen van beide interventies (er zijn dus 4 situaties: als de interventies A en B noemen en de controle O, dan zijn deze resp. AO, BO, AB en OO).
• 95% betrouwbaarheidsinterval of -confidence interval, 95% CI: het interval waarin een werkelijk gemiddelde met 95% zekerheid zich situeert ten opzichte van het gemiddelde bekomen in een bepaald experiment. Zo kan men zeggen dat wanneer men bij 100 mensen een bepaalde bloeddruk meet, het gemiddelde b.v.b. 140/90 mmHg bedroeg, maar dat de metingen varieerden, en dat moest men de ganse populatie kunnen testen (b.v.b. de bloeddruk van alle mensen ter wereld kunnen meten), dat deze met 95% zekerheid zou liggen tussen 130/80 mmHg en 150/100 mmHg (dit interval is het 95% CI).
• Absoluut risico, absolute risicostijging of -daling: absolute risico’s geven vaak een meer realistisch beeld dan relatieve risico’s. Stel dat een medicijn het risico op progressieve multifocale leukoencephalopathie (PML) verhoogt van 1 op 10 miljoen naar 1 op 1 miljoen. De absolute risicostijging is 9 op 10 miljoen maar het relatief risico is 10. Het laatste getal wordt vaak gebruikt in krantenkoppen: “Nieuw medicijn verhoogt kans op dodelijke hersenziekte met factor 10!”. Maar eigenlijk blijft het een zeldzaamheid, zeker wanneer het medicijn op een kleine schaal gebruikt zou worden. Bij frequente aandoeningen is de situatie omgekeerd. Stel dat een medicijn het risico op borstkanker verhoogt met een factor 1.10. Dat lijkt niet zo heel veel, maar als in een bepaalde populatie 10% van de vrouwen borstkanker krijgt, is de absolute risicostijging 1%. Dat wil zeggen dat voor elke 100 vrouwen dit behandeld worden, 1 extra geval van borstkanker zal ontstaan (zie number needed to harm).
• Bias: een of meerdere factoren die een objectieve interpretatie in de weg staan. Wetenschappelijke bias wil zeggen dat de interpretatie van studieresultaten verstoord kan worden. Culturele bias is b.v.b. het interpreteren van fenomenen door de bril van zijn eigen cultuur. Er bestaan verschillende vormen van wetenschappelijke bias, o.a.:
  • Completers bias: wanneer alleen die patiënten worden geanalyseerd die niet zijn uitgevallen tijdens de studie, worden alleen de “goede” patiënten geanalyseerd. B.v.b. een kankertherapie kan zeer effectief lijken als alleen de patiënten worden geanalyseerd die na een jaar nog naar het studiebureau kunnen komen. Degenen die de studie niet volbracht hebben zijn waarschijnlijk diegenen waarbij de interventie niet werkte.
  • Confirmation bias: het interpreteren van resultaten als een bevestiging van de algemeen aanvaarde hypotheses
  • Experimenter’s bias: het verkeerd interpreteren van de metingen door de persoon die het experiment uitvoert op basis van zijn/haar verwachtingspatroon. B.v.b. bij patiënten die een antihypertensivum krijgen wordt de bloeddrukmeting naar beneden afgerond, bij patiënten die placebo krijgen wordt naar boven afgerond. Dubbelblinde studies vermijden dit fenomeen.
  • Lead time bias: bias die ontstaat doordat er een langere inlooptijd aan een bepaalde groep wordt gegeven. Neem b.v.b. een ziekte met een slechte prognose zoals pancreaskanker. Stel dat we een groep patiënten onderwerpen aan een screeningstest voor pancreaskanker, en een andere groep niet. De patiënten bij wie de kanker wordt vastgesteld, zijn na 2 jaar allemaal overleden. De patiënten bij wie de ziekte pas ontdekt wordt in een symptomatisch stadium, zijn na 1.5 jaar allemaal overleden. Dat wil niet zeggen dat de screeningstest de overleving verlengt; de detectie gebeurt alleen vroeger. Een ander voorbeeld: stel dat we een groep kankerpatiënten chemotherapie geven en een andere groep niet. De groep die chemo krijgt moet eerst een port-a-cath krijgen, allerlei testen ondergaan enzovoort. Ondertussen sterven er enkele patiënten vooraleer ze chemo konden krijgen. Wanneer enkel de “sterkere” overlevers geanalyseerd worden, kan het lijken dat degenen die chemo kregen langer overleven.
  • Non-responders bias: bij enquêtes kunnen de leden van de populatie die antwoorden op een enquête b.v.b. grondig verschillen van diegenen die de enquête niet beantwoorden; hierdoor kan men de resultaten v.d. enquête moeilijk veralgemenen naar de ganse populatie.
  • Publicatiebias: als alleen die studies worden gepubliceerd waarin een positief resultaat werd gevonden, kan het lijken alsof geen enkele studie ooit een negatief resultaat vond. Dit kan het resultaat van een meta-analyse verstoren. Er bestaan echter statistische methodes om publicatiebias op te sporen. Een voorbeeld is de 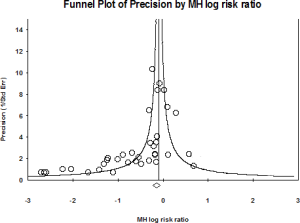funnel plot (zie afbeelding rechts). Dit is een grafiek waarbij elke studie in een meta-analyse wordt uitgezet, met op de X-as het relatief risico (voor- of nadeel van de interventie) en op de Y-as het omgekeerde van het 95% betrouwbaarheidsinterval (hoe groter en hoe nauwkeuriger de studie, hoe meer bovenaan). Er wordt verwacht dat kleinere, negatieve studies niet gepubliceerd geraken, waardoor onderaan de grafiek studies ontbreken aan één helft van de grafiek (rechts onderaan in het voorbeeld).
  • Recall bias: verstoring van de resultaten omdat patiënten zich bepaalde zaken anders herinneren dan de manier waarop ze in werkelijkheid gebeurt zijn. B.v.b. patiënt A kan zeggen dat hij veel sport gedaan heeft omdat hij vermagerd is en dus dat dit wel zal komen door veel te sporten, terwijl patiënt B zegt niet veel gesport te hebben omdat hij niet vermagerd is.
  • Response bias: wanneer bewust een verkeerd antwoord wordt gegeven, b.v.b. omdat men iets niet wil toegeven.
  • Selectiebias: verstoring van de resultaten doordat b.v.b. bepaalde patiënten meer kans hebben om geïncludeerd te worden in een studie. Patiënten die b.v.b. meedoen aan een studie kunnen meer gemotiveerd zijn dan anderen, wat de tolerantie of aanvaardbaarheid van de therapie hoger kan doen lijken.
• Case-control studie: een observationele studie waar men een groep met een bepaalde conditie (de ‘cases’) vergelijkt met een vergelijkbare groep zonder diezelfde conditie (de ‘controls’). Hiermee kan men epidemiologische risicofactoren voor een bepaalde aandoening opsporen. B.v.b. men vergelijkt patiënten met spontane bacteriële peritonitis met patiënten die ook ascites hebben maar geen peritonitis ontwikkelden, om te kijken of er bepaalde risicofactoren zoals medicaties geassocieerd zijn aan een verhoogde kans op deze vorm van peritonitis.
• Cluster randomized trial: studie waaraan verschillende onderzoekscentra of verschillende artsen deelnemen en waarbij niet de patiënten willekeurig in groepen worden ingedeeld, maar de behandelende centra of artsen. B.v.b. 10 huisartsen passen een techniek toe terwijl 10 andere huisartsen een andere techniek toepassen, of 10 ziekenhuizen gebruiken een protocol en 10 ziekenhuizen gebruiken geen protocol voor een bepaalde interventie.
• Cohort studie: studie waarbij een deel van een populatie (de cohorte) gedurende een bepaalde tijd (retrospectief of prospectief) bestudeerd wordt, dus met verschillende metingen tijdens een tijdsinterval, in tegenstelling tot een cross-sectionele studie waarbij de populatie op één ogenblik wordt bestudeerd.
• Confounder: een variabele die ervoor zorgt dat 2 populaties niet gelijk zijn en die mogelijk een gevonden effect geheel of gedeeltelijk kan verklaren. B.v.b. wanneer een behandeling zorgt voor een betere overleving, kan het zijn dat de patiënten die nog behandeld werden gewoon in betere algemene toestand zijn (in dat geval is hun algemene toestand een confounder).
• Cross-over: Engels voor overkruisen.
  • 1e betekenis: Sommige studies hebben een cross-over methodologie: dat wil zeggen dat b.v. de proefpersonen eerst aan experimentele conditie A worden blootgesteld en na een bepaalde tijd aan een andere experimentele conditie B. Dit kan nuttig zijn voor studies op kortere termijn (b.v. enkele weken) om het aantal personen in elke groep te verdubbelen, en om de proefpersonen te motiveren voor de studie door er voor te zorgen dat niemand ‘geluk’ of ‘pech’ kan hebben door in de ene of de andere groep geloot te worden (aangezien alle patiënten in zowel de interventie- als de controlegroep komen). Een ander voordeel is dat iedere persoon zijn eigen controlepersoon kan zijn, wat nuttig kan zijn voor metingen waarbij er een grote interindividuele spreiding is.
  • Soms is er een pauze (zgn. wash-out) tussen de twee studiecondities voorzien, waarbij b.v. een geneesmiddel de tijd krijgt om door het lichaam geklaard te worden zodat het niet meer aanwezig is in het tweede deel van de studie (voor deelnemers die eerst placebo krijgen wordt dan vaak dezelfde wash-out behouden, om de twee groepen aan gelijke condities bloot te stellen). Een wash-out kan ook voor (en na) de eigenlijke experimenten voorzien worden; vaak wil men immers dat er bepaalde andere medicatie gestopt wordt en de tijd krijgt het lichaam te verlaten vooraleer men een experimenteel medicijn probeert.
  • 2e betekenis: Van cross-over is ook sprake wanneer proefpersonen gerandomizeerd worden naar een bepaalde groep maar de procedure niet gevolgd wordt en de proefpersoon tóch wordt blootgesteld aan de experimentele condities van een andere groep (b.v. randomizatie naar afwachtende houding i.p.v. onmiddellijke chirurgie maar krijgt toch direct chirurgie op eigen initiatief, op initiatief van de behandelende arts, of wegens omstandigheden). Dit is de basis van het verschil tussen ‘intention-to-treat’-analyse en ‘per protocol’ analyse (zie verder). In dit geval is ‘overlopen’ een betere vertaling. Het is in deze betekenis een onopzettelijk fenomeen dat geen deel uitmaakt van het studieopzet en integendeel de analyse bemoeilijkt en dus onwenselijk is en best zo beperkt mogelijk blijft, maar vaak niet te vermijden is.
• Cross-sectionele studie: een observationele (niet-interventionele) studie die de leden van een bepaalde populatie op één welbepaald ogenblik bestudeerd. Hiermee kan men een prevalentie bepalen.
• 

  Auteur: Produnis. Licentie: cc-by-sa-3.0.

  Forest plot: (Nederlands: boomdiagram) is een grafiek die gebruikt wordt in meta-analyses om de individuele studies met hun confidence intervals, en hun gezamenlijke interpretatie, visueel weer te geven. In het voorbeeld hiernaast stellen de vierkantjes met strepen (zgn. box and whiskers, zeg maar een vierkant met snorharen) individuele studies voor. De grootte van elk vierkantje geeft de relatieve grootte van de studie weer (hoe meer deelnemers, hoe meer de studie doorweegt in de meta-analyse). De lijnen doorheen deze vierkanten (de “snorharen”) geven het betrouwbaarheidsinterval van elke studie weer. De ruit onderaan de grafie geeft het globaal effect weer op basis van de meta-analyse, met het betrouwbaarheidsinterval errond. De verticale lijn in de grafiek is de lijn van “geen effect” (ofwel een odds ratio van 1, ofwel een risk difference van nul). De bovenste twee grotere studies in het voorbeeld waren positief, de twee kleinere studies waren inconclusief (het betrouwbaarheidsinterval omvat de lijn van “geen effect).

• Funnel plot: zie publicatiebias.
• Heterogeniteit, I² van Higgins, inconsistentie: in een meta-analyse (zie hieronder) wordt uit verschillende studies een (gewogen) gemiddelde berekend. Nochtans is het ook belangrijk om te kijken in hoeverre de studies overeenkwamen (consistentie) dan wel elkaar tegenspraken (inconsistentie); eenzelfde gemiddelde heeft meer waarde wanneer de verschillende studies eerder hetzelfde aantoonden dan wanneer ze elkaar fel tegenspraken. De mate waarin studies elkaar “tegenspreken” noemt men heterogeniteit. Een goede maat voor heterogeniteit is de I²-waarde van Higgins (zie BMJ 2003). Dit geeft het percentage variatie tussen de studies weer dat niet door het toeval verklaart kan worden, of anders gezegd het percentage waarin de studies tot werkelijk verschillende resultaten kwamen. Alhoewel er geen echt grenspunt is voor ‘te veel’ heterogeniteit, kunnen we zeggen dat een lage, matige en hoge heterogeniteit overeenkomen met I²<25%, 25-50% en >50% (Minerva).
• Incidentie: het aantal mensen die in een bepaalde periode een bepaalde conditie ontwikkelt. Dit kan men onderzoeken in een longitudinale studie.
• Intention to treat analyse: In een gerandomizeerde studie is het wenselijk dat men de resultaten analyseert volgens de groepen waarin de patiënten werden toegewezen, ook al is er van het protocol afgeweken en kreeg de patiënt in werkelijkheid toch een andere behandeling. B.v. een patiënt wordt gerandomizeerd naar afwachtende houding i.p.v. onmiddellijke prostatectomie, maar hij verandert van mening en eist toch direct een operatie. In dat geval worden zijn gegevens toch best toegevoegd in de groep waarin hij werd toegewezen. Hierdoor komt het resultaat meer overeen met de klinische realiteit; het biedt namelijk een antwoord op de vraag “Wat is het verschil tussen het voorstellen van behandeling A en B?” i.p.v. “Wat is het verschil tussen het toepassen van behandeling A en B?”. In feite zijn beide vragen interessant maar de eerste vraag houdt rekening met b.v. de wensen van de patiënt en de mate waarin een bepaalde interventie aanvaardt of verdragen wordt. Deze analyse is ook het meest streng en objectief; er wordt enkel rekening gehouden met de randomizatie en niet met allerlei andere ‘excuses’ die achteraf kwamen. Zo blijft de randomizatie zuiver en zijn beide groepen in principe gelijkwaardig.
  • De omgekeerde analyse, waarbij de resultaten worden bekeken volgens de behandeling die de patiënt in werkelijkheid gekregen heeft, noemt men de per protocol analyse. Deze analyse is dus niet volgens de randomizatieprocedure verlopen en dus minderwaardig; bovendien gelden de resultaten alleen in een wereld waarin patiënten perfect de behandeling volgen zoals ze wordt voorgesteld door de arts.
  • Wanneer men in min of meer beperkte mate afwijkt van de strikte intention to treat analyse, spreekt men soms van een modified intention to treat analyse, hoewel deze term ambigu en af te raden valt.
• Longitudinale studie: een observationele (niet-interventionele) studie die een bepaalde populatie gedurende een bepaalde tijdsduur prospectief opvolgt. Hiermee kan men een incidentie bepalen.
• Meta-analyse: onderzoek waarbij de gegevens van verschillende studies samen statistisch worden geanalyseerd om tot een gemeenschappelijk besluit te komen (meestal waren de besluiten van de studies tegenstrijdig, of vonden sommige studies wél en andere geen effect). Wordt soms verkeerdelijk gezien als de hoogste vorm van evidentie, zonder beperkingen. Een meta-analyse is in de regel niet sterker qua evidentie dan de kwaliteit van de studies die ze bestudeert (uit een groep slechte studies kan je geen goed besluit trekken). Het resultaat hangt ook vaak af van welke studies wél en welke niet worden opgenomen in de meta-analyse (zo kunnen meta-analyses over hetzelfde onderwerp toch tegenstrijdige conclusies bereiken).
• Multipele vergelijkingen (multiple comparisons): wanneer men twee groepen vergelijkt op een hele reeks parameters, dan neemt de kans om een significant verschil te vinden toe met het aantal parameters dat men onderzoekt. Wanneer we b.v.b. een groep studenten in twee splitsen en we onderzoeken of zij verschillen voor een lijst van 100 parameters, dan is de kans groot dat er enkele parameters zijn waarin deze studenten ‘toevallig’ verschillen. Dit probleem doet zich b.v.b. voor bij genetisch onderzoek van grote groepen genen (zeker bij z.g.n. genoomwijde associatiestudies): stel dat we een 95% betrouwbaarheidsinterval als statistisch significant beschouwen, en we onderzoeken 10’000 genen, dan kunnen we louter op basis van toeval 500 nieuwe genen ontdekken voor een bepaalde ziekte! Dit is echter in de realiteit slechts toeval, dus geen echt verschil. Om dit op te lossen kan men afhankelijk van het aantal testen, het betrouwbaarheidsinterval kleiner maken of de P-waarde verkleinen: bij genoomwijde associatiestudies gebruikt men b.v.b. courant 1 x 10^–8.
• Number needed to harm (NNH): het aantal mensen dat een bepaalde interventie moet ondergaan om 1 schadelijk feit te veroorzaken. B.v.b. als 1 op de 200 patiënten een bloeding ontwikkelt met een bepaald geneesmiddel, is de NNH = 200.
• Number needed to treat (NNT): het aantal mensen dat een bepaalde behandeling moet ondergaan vooraleer 1 persoon er een gunstig effect van ondervindt. B.v.b. als een medicijn het risico op hartinfarct verlaagd van 2.5% naar 1.5%, is er een absolute risicodaling van 1% en een number needed to treat van 100.
• Odds ratio: dit geeft de verhouding weer tussen de kans op een gebeurtenis in één groep tegenover de kans in een andere groep. Het geeft de sterkte weer van een associatie tussen twee binaire variabelen. De odds ratio verschilt van het relatief risico (zie lager). Nemen we het voorbeeld van de Titanic, waarbij vrouwen en kinderen voorrang kregen voor de reddingssloepen:
  • van de 462 vrouwen waren er 308 die overleefden en 154 die stierven.
  • van de 851 mannen waren er 142 die overleefden en 709 die stierven.
  • voor vrouwen was de kans om te sterven op de Titanic 1 tegen 2 (154/308=0.5), en 5 tegen 1 (709/142=4.993) indien je een man was
  • de odds ratio is de verhouding van deze twee kansen: mannen hadden een bijna tien keer hogere kans om te sterven op de Titanic dan vrouwen (4.993/0.5=9.986)
  • het risico dat een vrouw stierf was echter 1 op 3 (154/462=33%); bij de mannen was dit 83,31% (=709/851).
  • het relatief risico is de verhouding tussen deze twee risico’s: mannen hadden een 2.5 keer groter risico om te sterven op de Titanic dan vrouwen (0.8331/0.3333).
  • Dit cijfervoorbeeld toont ook aan dat de odds ratio het risico kan overschatten. Stel dat we b.v. twee groepen hebben met een mortaliteit van 10% en 90%: het relatief risico bedraagt 9 maar de odds ratio bedraagt 81 (omdat de odds in de eerste groep 1 tegen 9 zijn en in de tweede groep 9 tegen 1; 9 gedeeld door 1/9 = 81). Het relatief risico leunt dichter aan bij hoe de mens logisch denkt, maar kan niet steeds in alle studiemethodes berekend worden (met name niet bij case-control studies, zie hoger). Enkel wanneer het zeldzame gebeurtenissen betreft, komt de odds ratio ongeveer overeen met het relatief risico. In beide gevallen kan de absolute risicostijging- of daling nog meer informatie geven (zie hoger).
• P-waarde: deze statistische waar drukt de kans uit dat een verschil in proporties tussen twee groepen (b.v.b. 6 op 10 in groep A en 15 op 20 in groep B, resp. 60% en 75%) verklaard kan worden door toeval. Hoe lager de P-waarde, des te kleiner de kans dat dit een toevallige vondst is. Hoe groter de populatie in de steekproef, hoe kleiner de P-waarde wordt. Zo kan een verschil tussen 65% en 69% statistisch significant zijn; dit zegt dus niets over de grootte van het verschil!
• Positieve predictieve waarde (PPW; positive predictive value, PPV): de kans dat een positieve test een werkelijk positief resultaat inhoudt. Dit wordt berekend door het aantal echt-positieven te delen door de som van de echt-positieven en de vals-positieven. Wanneer er dus veel vals-positieve waarden t.o.v. echt-positieve waarden zijn, neemt de PPW af. Dit hangt ook af van de prevalentie van een aandoening: bij een screeningstest voor een zeldzame ziekte wordt de kans op een vals-positieve waarde soms groter dan op een echt-positieve waarde.
• Prevalentie: het aantal leden van een bepaalde populatie die op een gegeven ogenblik een bepaalde conditie heeft. Dit kan men bepalen door een cross-sectionele studie.
• Propensiteit (propensity, propensity-matched analysis, propensity scores): propensiteit betekent neiging, overhelling. Stel dat we een groep patiënten bestuderen waarvan een deel een bepaalde therapie krijgt en een ander deel niet. Heel vaak zijn deze twee groepen niet gelijk voor meerdere variabelen. De kans dat ze behandeld worden kan toenemen wanneer voor deze variabelen aan bepaalde voorwaarden zijn voldaan (b.v.b. een patiënt met een COPD-opstoot kan meer kans hebben om met antibiotica behandeld te worden als hij koorts heeft, als hij thuis zuurstof krijgt, als hij snel ademt enz.). Aan deze voorwaarden kan men scores toekennen, zgn. propensiteitsscores. Men kan dan uit de ganse populatie twee groepen gaan samenstellen, die a priori evenveel kans hebben om behandeld te worden (=propensity matching). Dit is dus een manier om statistisch selectiebias tegen te gaan (zie onder bias). Bij een propensiteitsgewogen analyse vergelijkt men dus twee groepen waarbij de vooraf gekende variabelen gelijk zijn.
• Prospectief: de studie bestudeert en registreert feiten die zich nog moeten voordoen, m.a.w. hetgeen bestudeerd wordt vindt plaats nadat de studie is begonnen.
• QALY : afkorting van Quality-Adjusted Life Year. Dit wordt gebruikt om de kosten-effectiviteit van bepaalde interventies in te schatten. De levenskwaliteit als gevolg van een interventie wordt gegradeerd op een schaal van nul tot 1 waarbij 0 overlijden is en 1 perfecte gezondheid. Stel dat een bepaalde antitumorale therapie € 5 000 per jaar kost en leidt tot een verbetering van de levensverwachting met 6 maanden aan een gemiddelde levenskwaliteit van 0.5, dan bedraagt de prijs per QALY € 20 000. Niet alleen de levensverlenging maar ook de levenskwaliteit wordt dus in rekening gebracht. In elke maatschappij verschilt de grens van wat aanvaardbaar is als kost voor een QALY (met andere woorden welke interventie als kosteneffectief wordt beschouwd voor terugbetaling), maar deze liggen in de grootte-orde van waarden tot € 25 000 à € 40 000.
• Randomized controlled trial (RCT): een interventionele studie waarbij er willekeurig (ad random) werd bepaald of de interventie dan wel de controle werd toegepast. Het willekeurig indelen (de randomisatie) kan op verschillende manieren gebeuren, b.v.b. via geblindeerde enveloppes, via computerprogramma’s of telefooncentrales, enzovoort.
• Relatief risico (relative risk, RR, risk ratio): de verhouding tussen het risico dat een bepaalde gebeurtenis zich voordoet in een populatie i.v.m. het risico in de controlepopulatie. B.v.b. een relatie risico van 2.5 wil zeggen dat de kans op een gebeurtenis in de studiepopulatie 2.5 keer groter was dan de kans in de controlegroep. In klinische studies is het relatief risico vaak interessanter dan de odds ratio (zie hoger voor de verschillen en een cijfervoorbeeld).
• Retrospectief: de studie bestudeert en registreert feiten die zich afspeelden in het verleden, m.a.w. hetgeen bestudeerd wordt vond reeds plaats voor de studie begon.
• Screening harm: de nadelige gevolgen van screening, zoals overbehandeling van aandoeningen die anders niet behandeld zouden moeten worden (omdat de patiënt overlijdt aan een ander probleem vooraleer de gescreende aandoening een probleem wordt), vermijdbare psychologische belasting en schadelijke effecten van verdere (invasieve) onderzoeken voor vals-positieve resultaten.
• Sensitiviteit: de kans dat hetgeen met een bepaalde test opgespoord wordt ook werkelijk ontdekt wordt. Dit wordt berekend door het aantal (echt-)positieve testresultaten te delen door het werkelijk aanwezige aantal (= de som van de echt-positieven en de vals-negatieven).
• Specificiteit: de kans dat een negatief testresultaat ook werkelijk de afwezigheid betekent van hetgeen men onderzoekt (en niet omgekeerd, dus niet de kans dat een positief testresultaat correct is). Dit wordt berekend door het aantal echt-negatieven te delen door de som van de echt-negatieven en de vals-positieven. Theoretisch is een test die altijd een negatief resultaat weergeeft (er worden geen afwijkingen gedetecteerd) dus 100% specifiek.
• Statistische kracht (power), sample size: wanneer een studie een negatief resultaat bekomt, bestaat er steeds de mogelijkheid dat een positief resultaat gemist werd omdat de studie te klein was om een significant resultaat te vinden. Hoe groter de studie, hoe gemakkelijker het is om een positieve associatie vast te stellen wanneer er echt een bestaat, en hoe kleiner de kans dat een positieve associatie gemist wordt. Wanneer men op voorhand de variatie voor een bepaalde parameter kent (b.v. de pijnscores bij patiënten met een wervelindeuking variëren van 6-10, gemiddeld 8/10) en men op voorhand de grootte van het effect bepaalt dat men wil bekomen (een pijnstiller die de pijnscore met 2 punten kan verlagen), kan men op voorhand berekenen hoeveel patiënten men in een studie moet opnemen om met een bepaalde zekerheid (b.v. 85%) een gunstig effect van het medicijn te kunnen aantonen. Wanneer de studie dan geen significante verbetering kan vaststellen, is de kans nog 15% dat een grotere studie wél een significant verband zou kunnen vinden.
• Validiteit:
  • Interne validiteit verwijst naar de methodologische correctheid van een studie, waardoor ze kan besluiten dat er een causaal verband is tussen een interventie en een eindpunt of resultaat. Bias en confounding zijn twee voorbeelden van bedreiging voor de interne validiteit van een studie.
  • Met externe validiteit bedoelt men de mate waarin de resultaten van een studie van toepassing zijn op een reële doelpopulatie of patiëntengroep. Wanneer men b.v. heel veel exclusiecriteria heeft en zo een zeer specifieke patiëntengroep selecteert, zijn de resultaten van de studie enkel van toepassing voor patiënten die voldoen aan diezelfde criteria, en niet voor de patiëntenpopulatie in haar geheel.
  • Vaak is er een omgekeerde relatie tussen interne en externe validiteit: hoe methodologisch strenger een studie wordt, hoe groter de interne maar hoe kleiner de externe validiteit. Vaak probeert men daarom de resultaten van een studie met een grote interne validiteit, te repliceren in zgn. “real-world setting”, met andere woorden men gaat een minder strikte (b.v. observationele) studie opzetten om na te kijken of het effect dat bewezen werd in een experimentele setting (b.v. een klinische studie), ook kan geëxtrapoleerd worden naar de klinische, dagelijkse praktijk.
• Vals-negatief (false-negative): een negatief testresultaat terwijl er in werkelijkheid wél een aanwezigheid is van hetgeen waarvoor men test (b.v.b. een negatieve screeningstest terwijl er wél een onderliggende kanker is). Kan veroorzaakt worden door een gebrek aan sensitiviteit.
• Vals-positief (false-positive): een positief testresultaat zonder een werkelijke aanwezigheid van hetgeen men test (b.v.b. een positieve screeningstest zonder een echte onderliggende kanker). Kan veroorzaakt worden door een gebrek aan specificiteit.